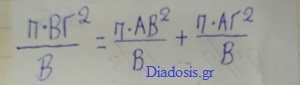Αν μια συνάρτηση είναι περισσότερων της μίας μεταβλητών, βρίσκουμε τις παραγώγους ως προς τις . . . . διάφορες μεταβλητές χωριστά και τότε αυτές λέγονται μερικές παράγωγοι.
Η μερική παράγωγος της[GLi]συνάρτησης f ως προς x συμβολίζεται με:

Π.χ. να βρεθούν οι παράγωγοι πρώτης και δεύτερης τάξης της συνάρτησης: f(x, ψ) = x3 + 4 x2ψ + ψ2x.
Οι παράγωγοι πρώτης τάξης είναι:
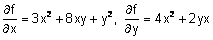
Οι παράγωγοι δεύτερης τάξης είναι:

Δηλαδή όταν βρίσκουμε τη μερική παράγωγο ως προς μια μεταβλητή, τις άλλες τις θεωρούμε σταθερές.